Parte 1
El objetivo de esta parte es poder generar nuestra primera imagen que será una esfera de color morado con fondo negro.
Para hacer esto vamos a ver las siguientes cosas:
- Cámara
- Ventana de vista
- Proyección
- Pantalla
- Raycasting
- Intersección con esfera
- Iluminación
Update: puedes ver un contenido similar a este en esta (presentacion en PyCon Chile 2022)
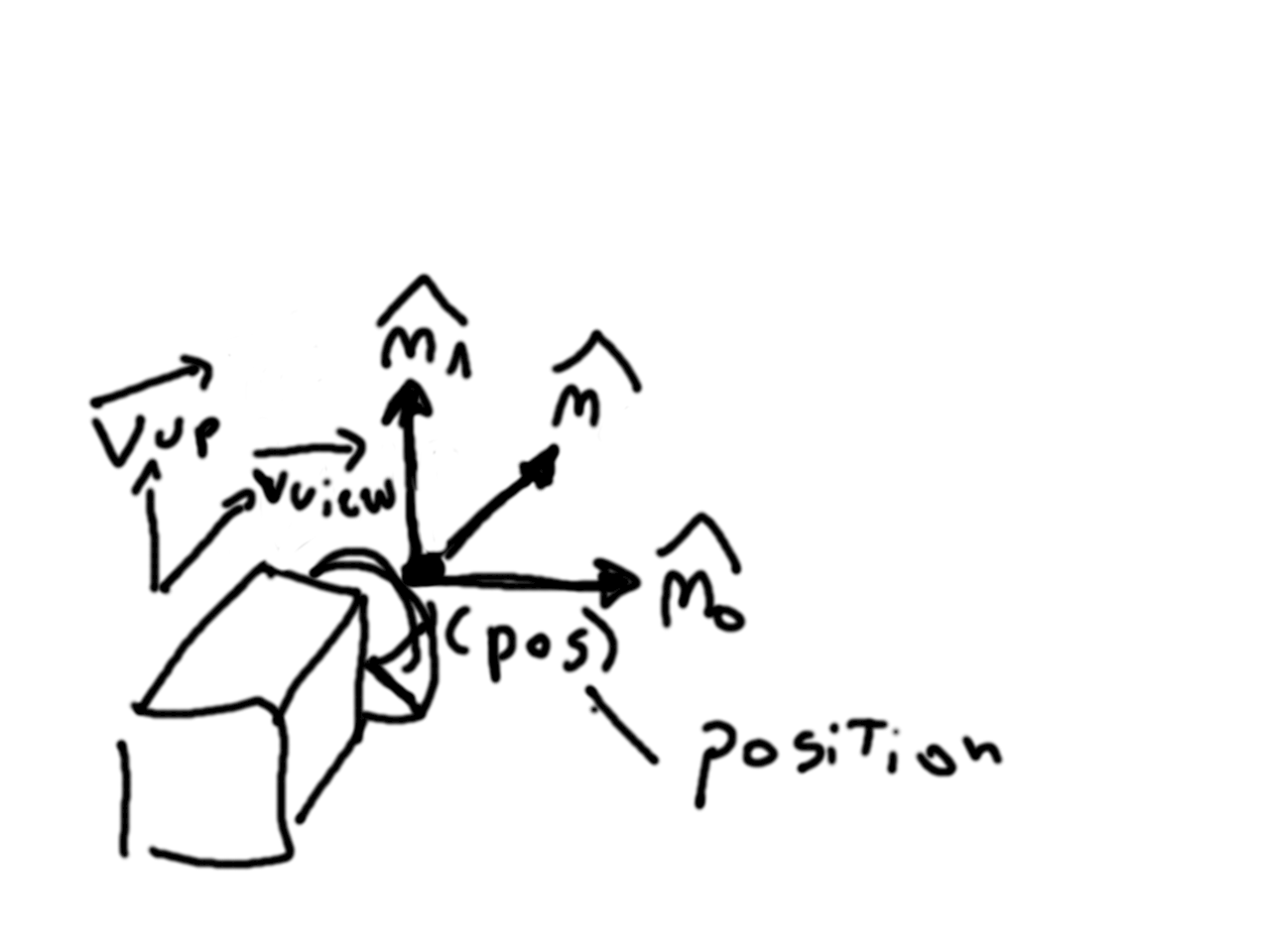
Para poder crear imágenes lo que hacemos es simular la realidad. Así que vamos a necesitar algo que simule el funcionamiento de una cámara. Algunos de los datos importantes de una cámara en particular son su posición en el espacio y su orientación. La posición es un punto en espacio tridimensional, y para la orientación generamos tres vectores unitarios y perpendiculares entre sí (n0, n1 y n2) que definen un espacio de coordenadas donde el lente de la cámara es el origen.
import numpy as np
import utils
class Camera:
def __init__(self, pos, v_up, v_view):
self.position = pos
self.n0 = utils.normalize(np.cross(v_view, v_up))
self.n1 = utils.normalize(np.cross(self.n0, v_view))
self.n2 = utils.normalize(np.cross(self.n1, self.n0))
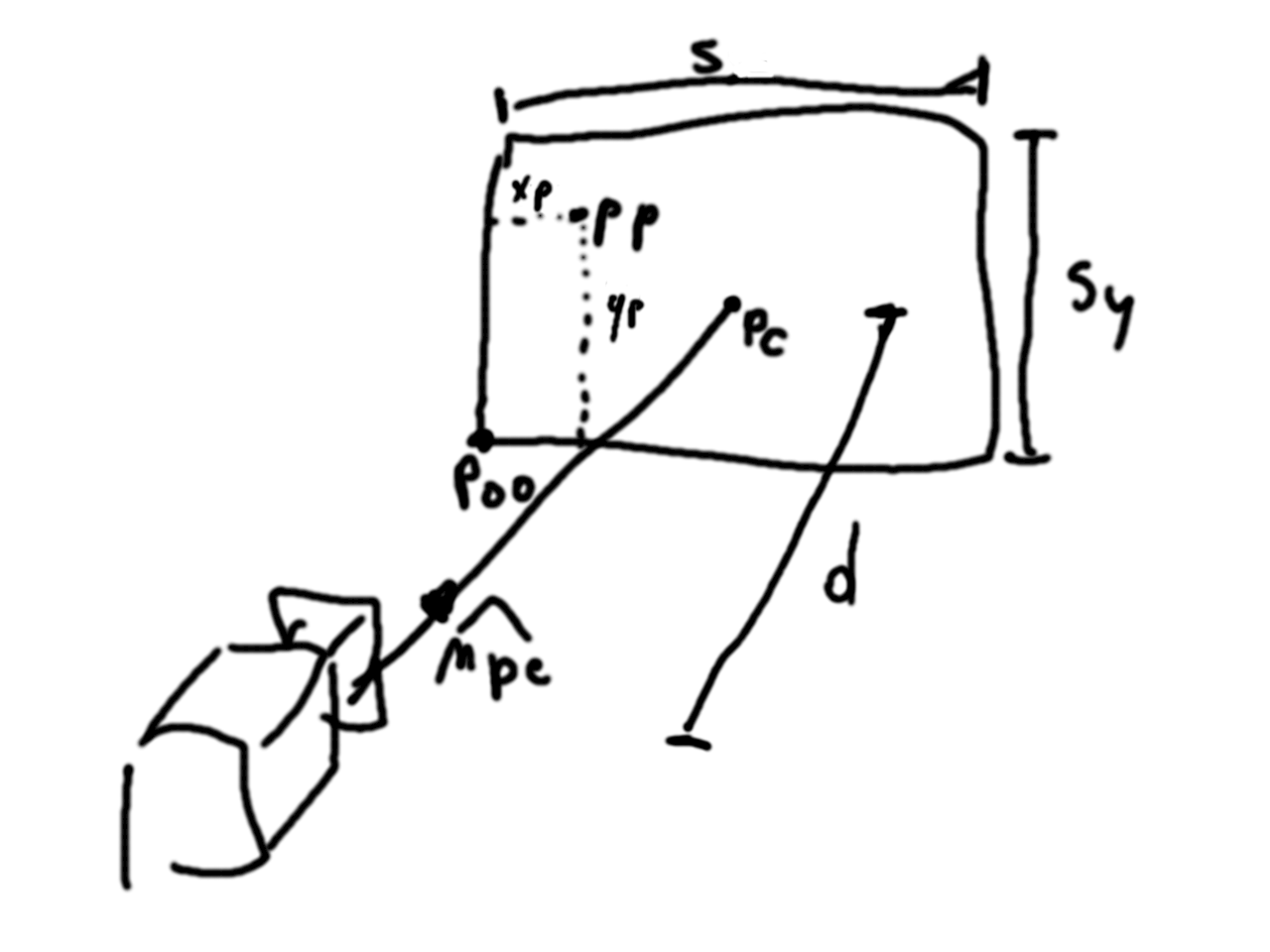
Luego podemos pensar en que todo lo que veremos en la pantalla al ver una imagen representa una ventana (un plano) en el mundo que estamos simulando. Suponemos que esta ventana está siempre al frente de nuestra cámara a una cierta distancia d y que tiene un ancho de sx y alto de sy. Luego podemos definir pc que es el punto justo al centro de la ventana y p00 que es el punto en la esquina inferior izquierda. Estos nos serviran posteriormente.
import numpy as np
import utils
class Camera:
def __init__(self, pos, v_up, v_view, d, sx, sy):
self.position = pos
self.n0 = utils.normalize(np.cross(v_view, v_up))
self.n1 = utils.normalize(np.cross(self.n0, v_view))
self.n2 = utils.normalize(np.cross(self.n1, self.n0))
pc = self.position + d * self.n2
self.p00 = pc - (sx / 2) * self.n0 - (sy / 2) * self.n1
self.d = d
self.sx = sx
self.sy = sy
Ahora el algoritmo de Raycasting usado en Raytracing consiste en disparar rayos desde el lente de nuestra cámara a, por lo menos, cada pixel que compone nuestra pantalla. La pantalla y la ventana, son dos cosas distintas. Nuestra ventana tiene dimensiones y posición dentro de nuestro mundo simulado, pero la pantalla es el espacio 2D donde vemos las imágenes que renderizamos. Entonces nuestra pantalla tiene cierta cantidad de pixeles en dirección horizontal y vertical.
Luego el código para generar una imagen es de la siguiente forma:
RGB_CHANNELS = 3
def render(scene, camera, height, width):
output = np.zeros([height, width, RGB_CHANNELS], dtype=np.uint8)
for j in range(height):
for i in range(width):
"""
- crear rayo entre lente y punto (i,j) en la ventana
- obtener el primer punto en que el rayo intersecta con un objeto
- obtener color para ese punto pp y asignarlo al pixel
"""
Así que vamos recorriendo la pantalla pixel por pixel, generando rayos… ¿Pero cómo generamos los rayos? Lo que cada rayo necesita es un punto de partida y un vector de dirección. El punto de partida podría ser el lente de la cámara o el punto donde el rayo intersecta la ventana, llamaremos a este punto pp. Luego el vector director npe es un vector unitario en la dirección en que va el rayo. Con esta información podemos generar nuestro rayo.
Ahora bien, para calcular pp lo que hacemos es mapear cada pixel de la pantalla a un punto en la ventana que estará definido en el mundo. Para eso calcularemos xp e yp que seran las posiciones horizontal y vertical del punto en la ventana. Luego el punto pp se define como la suma entre el punto p00, xp projectado en el eje n0 (de las coordenadas de cámara) y yp projectado en el eje n1.
RGB_CHANNELS = 3
MAX_COLOR = 255
def render(scene, camera, height, width):
output = np.zeros([height, width, RGB_CHANNELS], dtype=np.uint8)
for j in range(height):
for i in range(width):
xp = (i / width) * camera.sx
# we use height - 1 as the first value for y, because images
# start at the top pixel row
yp = ((height - 1 - j) / height) * camera.sy
pp = camera.p00 + xp * camera.n0 + yp * camera.n1
npe = utils.normalize(pp - camera.position)
ray = Ray(pp, npe)
color = raytrace(ray, scene)
output[j][i] = round(color * MAX_COLOR)
return output
Faltaría definir la clase Ray y la función raytrace. Para la primera pr será el punto donde el rayo inicia y nr el vector director.
class Ray:
def __init__(self, pr, nr):
self.pr = pr
self.nr = nr
def intersect_sphere(self, sphere):
# obtener el punto en que intersecta a la esfera o -1 si no lo hace
pass
También vamos a definir la clase esfera. Que tendrá una posición, un radio y un color simple.
class Sphere:
def __init__(self, pos, radius, color):
self.position = pos
self.radius = radius
self.color = color
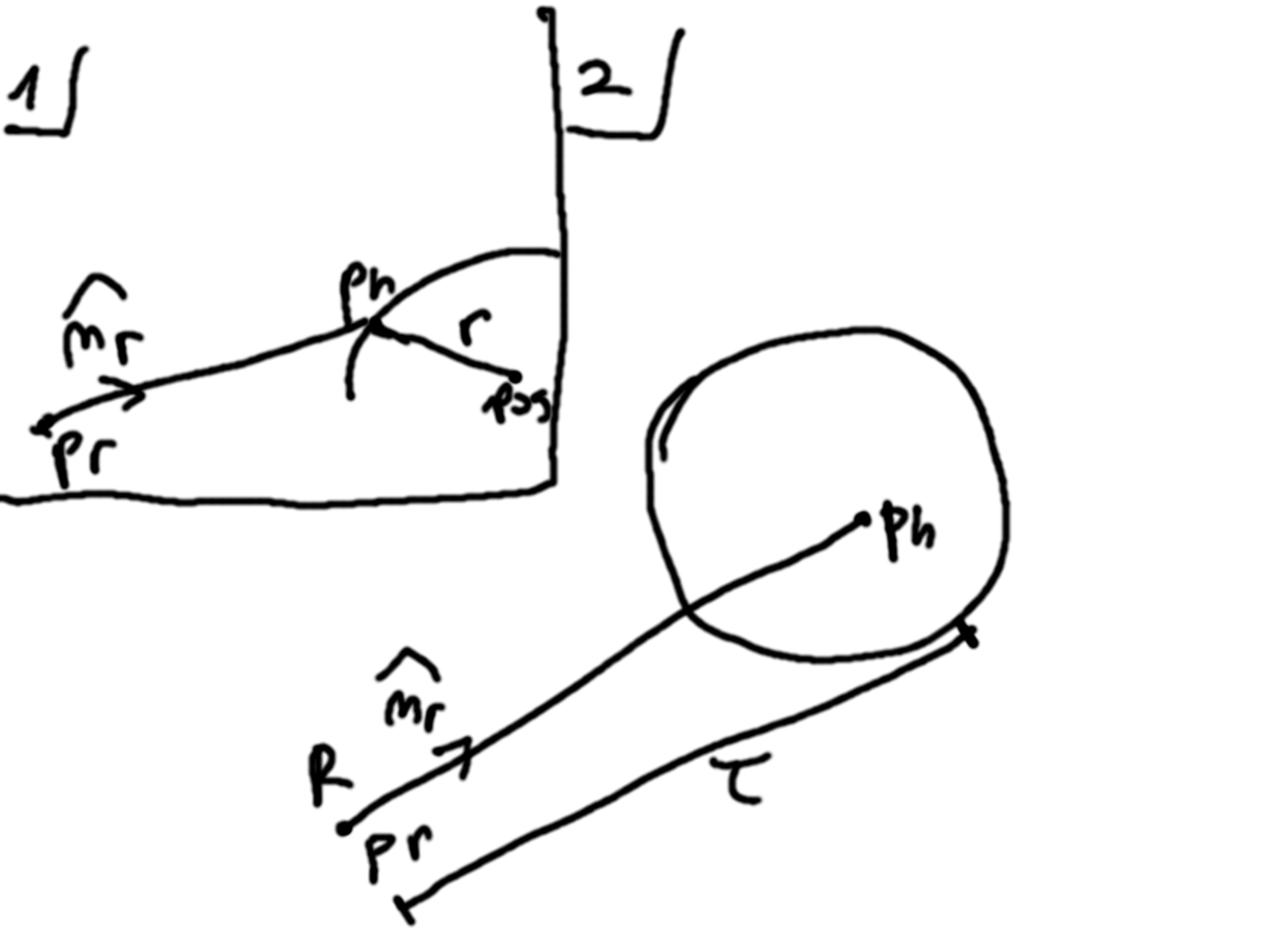
Ahora para intersectar esta esfera con un rayo vamos a hacer lo siguiente. Supongamos que existe un punto ph que es la primera intersección del rayo con la esfera (nota que podrían haber dos). Entonces ese punto, pertence tanto al rayo como a la esfera, y satisface las ecuaciones implícitas de ambas:
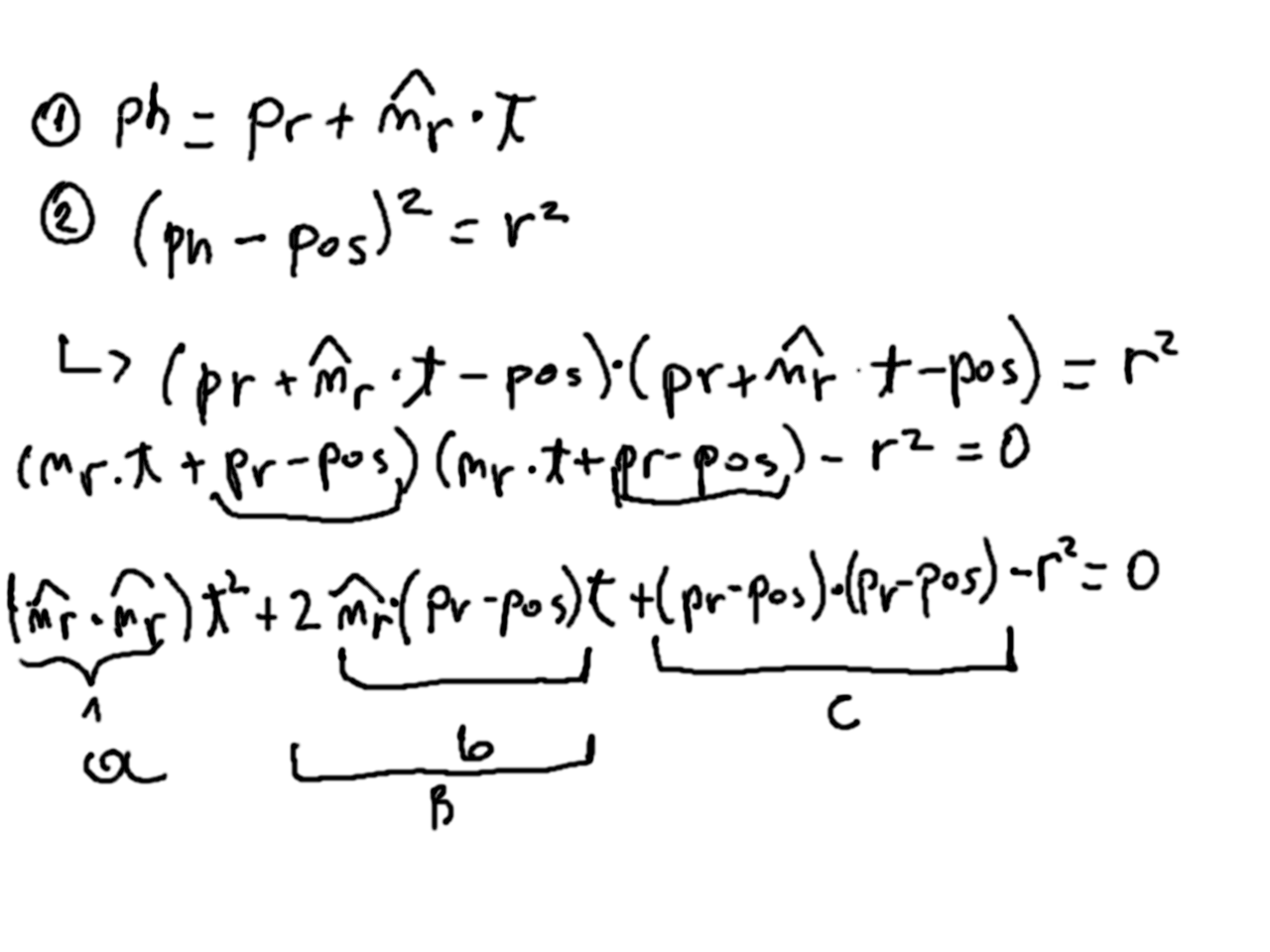
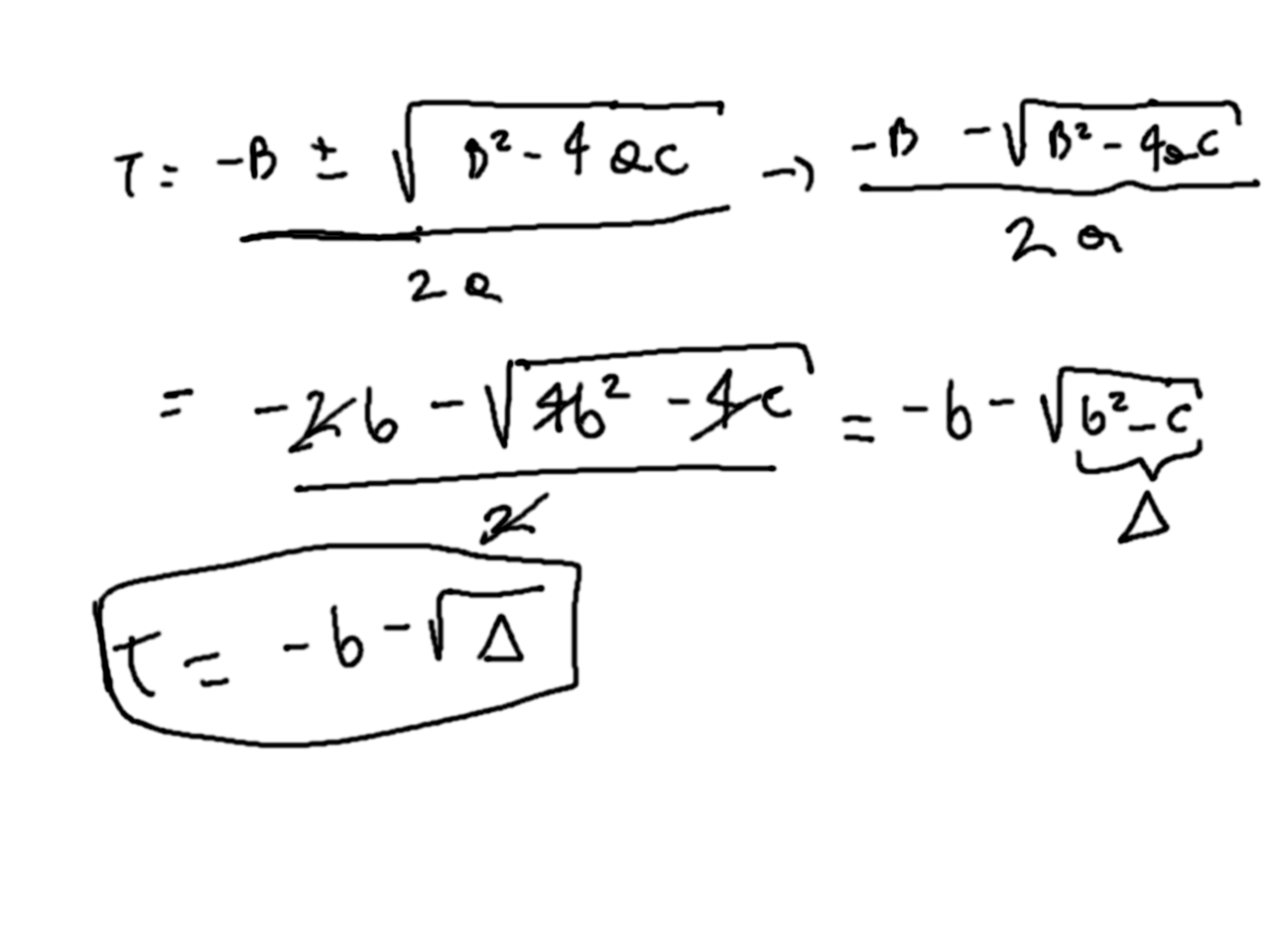
Finalmente nuestro código para intersectar queda así (el triángulo es discriminante):
class Ray:
def __init__(self, pr, nr):
self.pr = pr
self.nr = nr
def intersect_sphere(self, sphere):
pc = sphere.position
diff = self.pr - pc
b = np.dot(self.nr, diff)
c = np.dot(diff, diff) - sphere.radius ** 2
discriminant = b ** 2 - c
if b > 0 or discriminant < 0:
return -1
t = -1 * b - np.sqrt(discriminant)
ph = self.pr + t * self.nr
return ph
También nos queda nuestra función de raytrace que se preocupa de simular la iluminación. Ésta recibe un rayo y una esfera y se preocupa de devolver el color que se asignará si el rayo intersecta la esfera.
RGB_CHANNELS = 3
def raytrace(ray, sphere):
ph = ray.intersect_sphere(sphere)
if ph:
return sphere.color
else:
return np.zeros(RGB_CHANNELS)
Ahora si usamos esto, nuestro programa nos devolverá un círculo con color completamente igual, para que se vea 3D es necesario simular mejor la iluminación. Así que vamos a simular una luz que está en el mundo en una posición específica.
class PointLight:
def __init__(self, pos):
self.position = pos
Para calcular color lo que hacemos en el punto ph es generar un vector unitario en dirección a la luz. Si la normal de la superficie en el punto apunta cerca de la luz quiere decir que la recibe más directamente, por ende estará mejor iluminada y reflejará más el color del objeto. Por el contrario si la normal apunta hacia otro lado quiere decir que le llega menos o no le llega luz. Esto lo podemos ver con el producto punto o coseno entre el vector que apunta a la luz y la normal (ojo, ambos unitarios). Llamaremos l al vector que apunta a la luz, y agregaremos una función en la clase esfera que nos entregue la normal para un punto en la esfera.
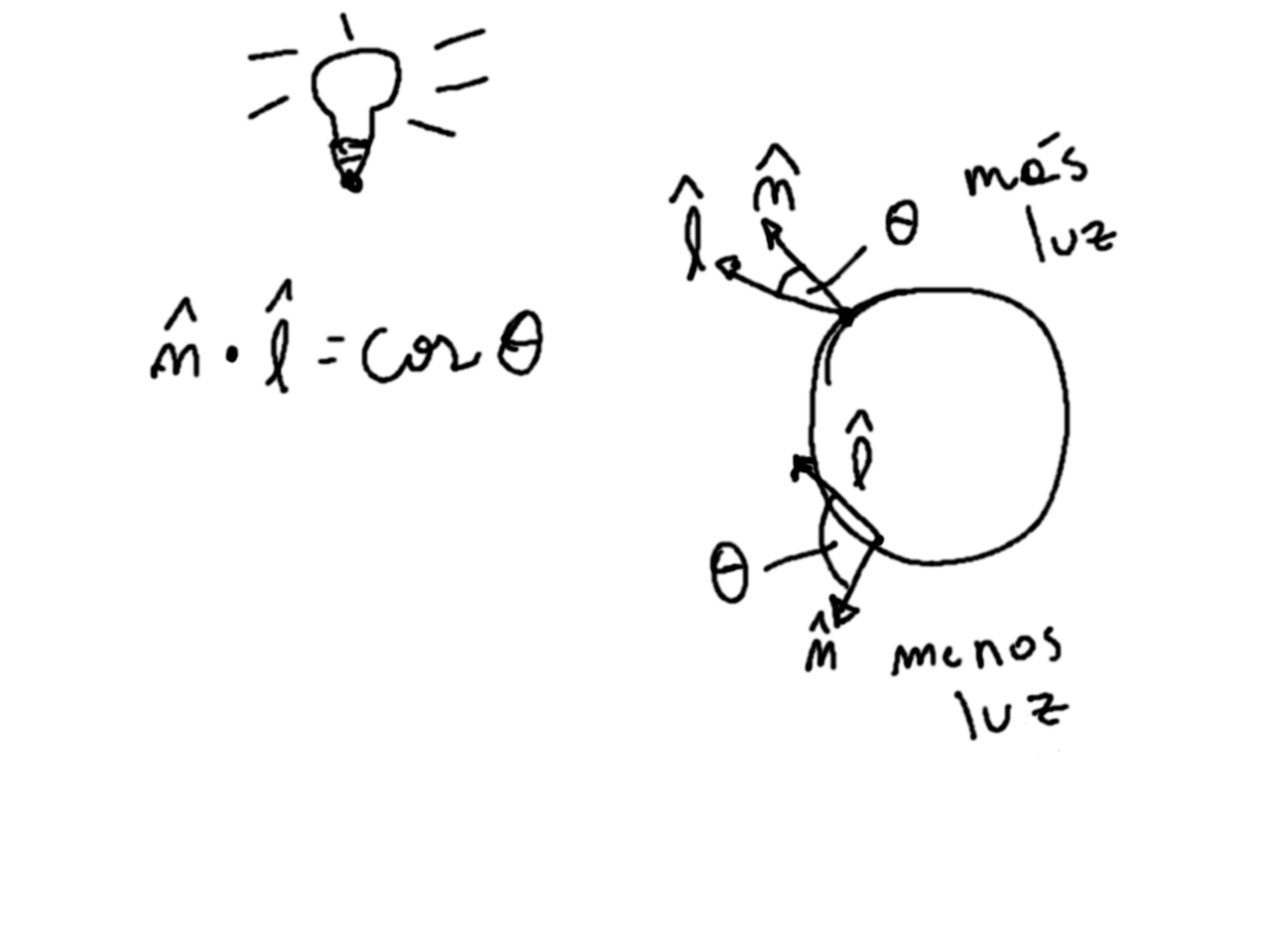
class Sphere:
def __init__(self, pos, radius, color):
self.position = pos
self.radius = radius
self.color = color
def normal_at(self, p):
n = (p - self.position) / self.radius
return n
RGB_CHANNELS = 3
def raytrace(ray, sphere, light):
ph = ray.intersect_sphere(sphere)
if ph:
n = sphere.normal_at(ph)
l = utils.normalize(light.position - ph)
diffuse_coef = np.dot(n, l)
t = max(0, diffuse_coef)
color = t * sphere.color
return color
else:
return np.zeros(RGB_CHANNELS)
Y también tendremos que cambiar nuestro llamado a raytrace que hacemos desde render, ya que por ahora no vamos a definir una clase escena (lo haremos después).
RGB_CHANNELS = 3
MAX_COLOR = 255
def render(sphere, light, camera, height, width):
output = np.zeros([height, width, RGB_CHANNELS], dtype=np.uint8)
for j in range(height):
for i in range(width):
xp = (i / width) * camera.sx
# we use height - 1 as the first value for y, because images
# start at the top pixel row
yp = ((height - 1 - j) / height) * camera.sy
pp = camera.p00 + xp * camera.n0 + yp * camera.n1
npe = utils.normalize(pp - camera.position)
ray = Ray(pp, npe)
color = raytrace(ray, sphere, light)
output[j][i] = round(color * MAX_COLOR)
return output
Voilà! Tenemos todo lo necesario para generar nuestra primera imagen. Nuestro programa principal lucirá así:
from PIL import Image
import numpy as np
# local modules
from camera import Camera
from light import PointLight
from render import render
from sphere import Sphere
OUTPUT_FILENAME = "img.png"
MAX_COLOR_VALUE = 255
def main():
# Create sphere
sphere_pos = np.array([0, 0, 1.5])
sphere_rad = 0.4
color_purple = np.array([75 / MAX_COLOR_VALUE, 0, 130 / MAX_COLOR_VALUE])
sphere = Sphere(sphere_pos, sphere_rad, color_purple)
# Create light
light_pos = np.array([0, 1.5, 0])
light = PointLight(light_pos)
# Create camera
camera_pos = np.array([0, 0, 0])
v_up = np.array([0, 1, 0])
v_view = np.array([0, 0, 1])
d = 0.035
width_ratio = 16
height_ratio = 9
aspect_ratio = width_ratio / height_ratio
sy = d
sx = sy * aspect_ratio
camera = Camera(camera_pos, v_up, v_view, d, sx, sy)
pixel_scale = 20
width = width_ratio * pixel_scale
height = height_ratio * pixel_scale
img_arr = render(sphere, light, camera, height, width)
img = Image.fromarray(img_arr)
img.save(OUTPUT_FILENAME)
print(f"Image saved in {OUTPUT_FILENAME}")
if __name__ == '__main__':
main()
Lo que produce una imagen final como esta 🙂:
